Movimientos circulares (II)

En una carrera de F1 vemos cantidad de curvas (con aceleración normal) en las que además cambia el valor de la velocidad (aceleración tangencial).
Las dos aceleraciones las sufre el piloto. De esta forma la cabeza (y el resto del cuerpo) de Fernando Alonso se ve sometido a aceleraciones adelantes y atrás producidas por las frenadas o acelerones y aceleraciones a los lados producidas por las curvas.
Los valores de estas aceleraciones se pueden calcular con las fórmulas:

Aceleración tangencial:    a_t = (v_f-v_i)/t   dirección movimiento

Aceleración normal:          a_n= v²/R   dirección perpendicular

Podemos hacer una simulación esquemática de una curva en un circuito y calcular las aceleraciones del coche y del piloto. Estas aceleraciones suelen venir representadas en gráficos que se incluyen en las representaciones. Hay que tener en cuenta que:

aceleración tangencial positiva:   es responsable el motor

aceleración tangencial negativa .  es responsable el freno

aceleración normal:   es responsable la inclinación de la pista (peralte) y el sistema de dirección.

Vamos a calcular las aceleraciones en el tramo de frenado, en la curva y en el tramo final.

Tramo de frenado en recto.

No tiene aceleración normal porque es una recta.

Tiene aceleración tangencial ya que va frenando:   at= (40-90)/8 = - 6,25 m/s2

En la curva.

Tiene aceleración normal dirigida hacia el centro de la curva  an=v2/R= 2500/300=8,33 m/s2

Tiene aceleración tangencial ya que esta acelerando un poco at= (50-40)/2= 5m/s2

La aceleración total hay que dibujarla y calcularla por el Teorema de Pitagoras:

a²= a_t² + a_n² = 8,33² + 5² = 94,38  a=9,71 m/s²

En el tramo final

No tiene aceleración normal porque es una recta.

Tiene aceleración tangencial ya que:   at= (80-60)/4 =  5 m/s2

En la fórmula 1 los puntos más comprometidos para el coche y el piloto son las curvas rápidas. En ellas se lleva al límite la resistencia de todos los componentes del coche y de su conductor.

Cuestión:

Problema 2:

Un coche realiza un recorrido como el de la figura con las velocidades siguientes:

V_a=30m/s  t=0

v_b=4Om/s  t=10s

v_c=40m/s  t=20s

V_d=30m/s  t=30s

v_e=2Om/s  t=40s

Calcular y dibujar la aceleración normal, tangencial y total en los puntos b y e.

Movimientos circulares.

Comenzamos con el más sencillo.
Movimiento circular uniforme.
 En ese movimiento el objeto gira con la misma velocidad una trayectoria circular de radio R. Podemos estar en un coche en una rotonda manteniendo la velocidad, la ropa en una lavadora centrifugando, en una atracción de feria o los propios planetas o satélites.


Si dibujamos la velocidad en este movimiento:
 La velocidad tiene el mismo valor pero va cambiando continuamente de dirección. El objeto tiene aceleración, pero esta aceleración únicamente cambia la dirección de la velocidad.


Es una aceleración dirigida hacia el centro del movimiento que se llama aceleración normal o centrípeta.

Se calcula con la fórmula      a_n= v²/R.
Esta aceleración es producida por una fuerza que sienten los pilotos de F1, la ropa en una lavadora o nosotros mismos al estar sentados en un coche tomando una curva.

Cuestiones:
1. Tomamos una rotonda  de 20 m de radio a 100 km/h. ¿Qué aceleración tiene el coche? Compararla con la aceleración de la gravedad.

2. Una lavadora puede girar cuando centrifuga a 1000 rpm (vueltas por minuto).  ¿Que aceleración sufre la ropa? Si te falta algún dato utiliza tu cabeza para encontrarlo.

3. Un satélite de comunicaciones gira en torno a la Tierra en una órbita de radio 42000 km. Da una vuelta cada día (para estar siempre en el mismo punto respecto a nosotros). ¿Qué aceleración tiene?. 

Problemas de caída sin rozamiento.

6.         Lanzamos un objeto desde el suelo hacia arriba con una velocidad de 25 m/s.

a.    Qué velocidad y posición tiene al cabo de 2 segundos?

b.    Puedes calcularlo también a los 4 segundos?

c.    Cuanto tiempo tarda en llegar a la altura máxima?

d.    Calcula la máxima altura a la que llega.

Croquis del problema:

Al cabo de 2 segundos. Ecuaciones del movimiento:

v= vi  + a.t  = 25 + (-9,8).2 = +17,2 m/s   está subiendo

x= xi + vi.t + 0,5.a.t2 = 0 + 25.2 + 0,5. (-9,8).4 = 30,4 m  está a 30,4 m de altura

Al cabo de 4 segundos. Ecuaciones del movimiento:

v= vi  + a.t  = 25 + (-9,8).4 = -14,2 m/s   está bajando ya después de llegar a lo más alto

x= xi + vi.t + 0,5.a.t2 = 0 + 25.4 + 0,5. (-9,8).16 = 21,6 m  está 21,6 m de altura no ha llegado al suelo todavía

Altura máxima:

En el punto de altura máxima su velocidad es 0.   v= vi  + a.t  = 25 + (-9,8).t = 0

t=2,55 s  lo que está de acuerdo con el apartado anterior.

La altura en ese momento será:

x= xi + vi.t + 0,5.a.t2 = 0 + 25. 2,55 + 0,5. (-9,8). 6,50= 31,87 m 

7.         Un globo se encuentra a 80 m de altura. Cuanto tiempo tardará en llegar al suelo un objeto que dejamos caer desde el globo si:

a.    el globo está parado.

b.    el globo baja a 2 m/s.

c.    el globo asciende a 2 m/s.

Globo parado: velocidad inicial 0m/s posición inicial 80 m, posición final 0 m.

 Ecuaciones del movimiento:

x= xi + vi.t + 0,5.a.t2 = 80 + 0.t + 0,5. (-9,8). t2 = 0   t=4,04 s.

Globo subiendo: velocidad inicial  +2m/s posición inicial 80 m, posición final 0 m.

 Ecuaciones del movimiento:

x= xi + vi.t + 0,5.a.t2 = 80 + 2.t + 0,5. (-9,8). t2 = 0   t= 4,20 s. Este tiempo incluye la subida del objeto al soltarlo ya que al principio el objeto sube con el globo.

Globo bajando: velocidad inicial -2m/s

 posición inicial 80 m, posición final 0 m.

 Ecuaciones del movimiento:

x= xi + vi.t + 0,5.a.t2 = 80 + (-2).t + 0,5. (-9,8). t2 = 0   t=3,80 s.

En este caso tarda menos ya que desde el principio el objeto lleva una velocidad hacia abajo.

                                                                                                                                                                                                                                                                                                                                                

8.       Javier Sotomayor era el campeón de salto de altura con una marca de 2,45 m. Determina la velocidad con la que saltó verticalmente desde el suelo (velocidad de salida). Supón despreciables los efectos del rozamiento con el aire.

Altura máxima: V final= 0

Ecuaciones del movimiento:

v= vi  + a.t ;  0 = v + (-9,8).t    v= 9,8.t

x= xi + vi.t + 0,5.a.t2 ;   2,45 = 1,10 + v.t + 0,5. (-9,8). t 2

Sustituyo en la segunda ecuación  2,45=1,10 + 9,8.t.t - 4,9.t2   1,35= 4,9.t2  t=0,52s

El campeón olímpico tarda en llegar al punto más alto de su salto 0,52s

La velocidad con la que despegó del suelo será:  v=9,8.t = 5,14m/s =18,5km/h

Otros tres problemas resueltos.

10.     Observa las gráficas siguientes. Tienes que sacar de cada una la máxima información posible del movimiento que representa.

Gráfica 1. Se trata de un objeto que tiene diferentes velocidades. Desde 0 a 3 s va aumentando su velocidad progresivamente desde 0 hasta 6 m/s. En tres segundos deja de acelerar y se limita a mantener la velocidad. A los 6 segundos comienza a frenar y su velocidad va descendiendo. Se detiene en dos segundos más.

Podría ser por los valores de velocidades y tiempos una bicicleta arrancando, manteniendo la velocidad y frenando.

Gráfica 2. En la gráfica dos tenemos un objeto que sale del punto 0 y llega al punto x=6 en 2 s. Pero este movimiento no es uniforme, primero va despacio y luego va deprisa. Es un movimiento acelerado. En el punto 6 ocurre algo extraño ya que se para de repente. Durante dos segundos más está parado en x=6 (tal vez fruto de una caída).  Desde el segundo 4 hasta el segundo 8 vuelve lentamente hasta el punto x=0. Va retrocediendo (su velocidad será negativa), tarda 6 segundos al punto de partida. Tal vez se lesiono en la caída y tenga algún problema.

Gráfica 3. Este movimiento comienza con una velocidad de 3m/s. La velocidad aumenta (acelera) hasta v=9m/s. Tarda en acelerar 4s.

Gráfica 4. Este movimiento comienza con una velocidad de 8 m/s. La velocidad va disminuyendo (aceleración negativa o frenado) hasta que el objeto se para en t=6s.

13.     (PAU junio 02) La figura representa la gráfica «velocidad - tiempo» para un cuerpo que se mueve sobre una recta y que sale del reposo. Razona si el espacio recorrido por el móvil en el intervalo de tiempo durante el cual aumenta su velocidad es mayor , más pequeña o al igual que el espacio recorrido durante la frenada.

El movimiento consiste en acelerar desde 0 a 30 m/s en 6 segundos y después una frenada de 30m/s a 0 en otros 6 segundos.

El espacio recorrido en cada caso lo podemos hacer utilizando la velocidad media.

En el primer tramo la velocidad media ha sido (0-30) 15 m/s  y el tiempo 6 s------- 90m

En el segundo tramo la velocidad media ha sido (30-0) 15 m/s  y el tiempo 6 s------- 90m

los espacios recorridos han sido iguales.

23.     Un coche y un camión están separados 50 metros. El camión se mueve con una velocidad constante de 54 km/h mientras que el coche, que está inicialmente parado, arranca con una aceleración de 1,6 m/s² que mantiene constante.

a.    Cuanto tiempo tardará el coche en atrapar al camión?

b.    En qué posición estarán entonces?

c.    Qué velocidad llevará el coche en este instante?

d.    Haz las gráficas a-t, v-t y x-t de los dos movimientos.

El coche aunque está parado al principio va ganando velocidad, llegará un momento en que vaya más deprisa que el camión y por tanto al final lo alcanzará.

Las ecuaciones del movimiento del coche y del camión serán:

camión   x= 50 + 15 t

coche  x= 0 + 0.t + 1/2 . 1,6 . t2     se resuelve y el resultado es t=2,16s  y x=373m

la velocidad del coche en ese momento será mayor que la del camión   v=0+1,6 .2,16  =34,5m/s

                                                                                                                                                                                                                                                                                                               

Seguimos haciendo problemas de movimientos y hay van tres ejemplos resueltos:

4.         Un coche hace un trayecto según la siguiente gráfica v-t. Sabemos que en el instante inicial su posición es cero.

a.    Describe verbalmente el movimiento.

b.    Calcula la posición de este coche al término de cada intervalo de tiempo (siempre respecto al origen).

c.    Construye la gráfica posición-tiempo correspondiente.

d.    Cuál ha sido su desplazamiento?

e.    Qué velocidad media ha mantenido?

Observamos la gráfica. Sabemos que en el instante inicial la posición es x=0.

Durante 100 s lleva una velocidad 30, después 100s a 30, después 100 s a -20(vuelve hacia atrás)y después otros 100 s a 20. Es una sucesión de movimientos uniformes encadenados. No hay aceleración.

1 tramo:

x= xo + v.t = 0 + 100.30 = 3000m.   Esta fase acaba en 3000m

2 tramo:

x= xo + v.t = 3000 + 100.20 = 5000m.   Esta fase acaba en 5000m

3 tramo:

x= xo + v.t = 5000 + 100.(-20) = 3000m.   Esta fase acaba en 3000m

4 tramo:

x= xo + v.t = 3000 + 100.20 = 5000m.   Esta fase acaba en 5000m

9.         A las 9 horas de la mañana pasa por una estación de servicio un vehículo robado con una velocidad constante de 90 km/h. A los diez minutos pasa por el mismo punto un coche de la policía persiguiendo al primero con una velocidad de 126 km/h.

a.    Cuanto tiempo tardará la policía en detener a los ladrones?

b.    En qué posición tendrá lugar la detención?

c.    Haz las gráficas v-t y x-t de los dos coches.

Cuando sale el policía, el ladrón lleva 10 minutos de ventaja lo que es equivalente a 15 Km o 15000. La velocidades en m/s son 35 y 25. El policía irá recortando distancia hasta que alcance al ladrón. Escribirmos las ecuaciones del movimiento del ladrón y del policía (no tienen aceleración)

ladrón   x= 15000 + 25 t      policía  x= 0 + 35t    resolvemos el sistema:

t=1500s  y x= 52500m = 52,5 km

19.     Se llama tiempo de reacción al que transcurre desde que un conductor observa un obstáculo hasta que pisa el pedal del freno. Normalmente es de algunas décimas de segundo.

Supon que la velocidad que lleva es de 90 km/h, el tiempo de reacción es de 0,4 segundos y que la aceleración de frenada es de -3 m/s².

a.    Calcula el espacio necesario para quedar parada.

b.    Representa las gráficas a-t, v-t y x-t del movimiento.

En la primera parte de la frenada el conductor todavía no ha reaccionado. Durante 0,4 s, no frena y lleva movimiento uniforme.

Después pisa el freno y el coche pierde velocidad hasta que finalmente se detiene. En esta fase hay que calcular cuanto tiempo tarda en detener el coche y después podemos calcular la distancia recorrida.

1ºFase. 90 km/h= 25 m/s    x= 0 + 25. 0,4= 10 m  mientras reacciona

2º fase.  Tiempo que tarda en detenerse.  v= v0+at   

0 = 25 + (-3).t  t=8,3s

 y la posición final  x= xo + vm.t = 10 + (12,5).8,3 = 218 m

también lo podemos hacer con la fórmula x= xo + vo.t + 1/2.a.t2

5º clase. Movimientos rectilíneos.

Puedes consultar este otro problema resuelto.

De los problemas siguientes intenta hacer cinco de los diferentes tipos. Vienen las soluciones para que compruebes.

Ejercicios de movimientos rectilíneos acelerados

EJERCICIOS: Proceden de Tabi Casellas  www.fislab.net 2.         Mirando la representación gráfica, a.    Describe verbalmente el movimiento del coche en los diferentes tramos del recorrido. b.    Calcula la velocidad de cada intervalo. c.    Representa la correspondiente gráfica v-t. d.    Calcula la velocidad media de todo el recorrido.                                                                                                                                                                                                                                                                                                                                      Resultado:       2,5 m/s 5 m/s 0 m/s - 7,5 m/s -3,75 m/s 3.         El movimiento de un coche viene representado por la siguiente gráfica posición-tiempo. a.    Explica el movimiento de este automóvil. b.    Calcula la velocidad en cada tramo. c.    Haz la gráfica v-t que le corresponde. d.    En qué instantes el coche está en la posición 200 m? e.    Encuentra la velocidad media del movimiento. f.      Cuál es la velocidad media hasta los 50 segundos?                                                                                                                                                                                                                                                                                                                                        Resultado:       15 m/s - 10m/s 40m/s 5 m/s 13,3 s 30 s y 55 s 5 m/s y 6,6 m/s 4.         Un coche hace un trayecto según la siguiente gráfica v-t. Sabemos que en el instante inicial su posición es cero. a.    Describe verbalmente el movimiento. b.    Calcula la posición de este coche al término de cada intervalo de tiempo (siempre respecto al origen). c.    Construye la gráfica posición-tiempo correspondiente. d.    Cuál ha sido su desplazamiento? e.    Qué velocidad media ha mantenido?                                                                                                                                                                                                                                                                                                                                     Resultado:      3.000 m 5.000 m 4.000 m 5.000 m 125 m/s 5.         En un punto de una carretera se han cruzado dos vehículos que marchan en sentidos contrarios. El primero lleva una velocidad de 54 km/h y el segundo de 36 km/h. a.    Cuál será la distancia que los separará a los 45 minutos? b.    Representa las gráficas v-t y x-t de los dos movimientos. c.    Comprueba el resultado de la primera pregunta en la gráfica posición-tiempo.                                                                                                                                                                                                                                                                                                                         Resultado:            67.500 m 6.         Dos pueblos, Girona y Quart, están separados por una distancia de 5 km. Una carretera recta los une. Un peatón sale de Girona hacia Quart caminando con una velocidad de 3,6 km/h. a.    En qué posición estará al cabo de 3 horas? b.    A qué distancia se encontrará de Girona? c.    Y a qué distancia de Quart estará en este momento?                                                                                                                                                                                                                                                                                                                         Resultado:            10.800 m 5.800 m Si en lugar de caminar hacia Quart lo hace en sentido opuesto, d.    A qué distancia estará de Girona al cabo de tres horas? e.    Y qué distancia el separará de Quart?                                                                                                                                                                                                                                                                                                                         Resultado:            10.800 m 15.800 m 7.         Dos coches están separados 1.000 m en una recta de la autopista. Los dos se mueven con velocidades constantes de 126 km/h y 72 km/h con sentidos contrarios hasta encontrarse. a.    Cuanto tiempo tardaran en encontrarse? b.    En qué posición tendrá lugar el encuentro? c.    Dibuja las gráficas v-t y x-t.                                                                                                                                                                                                                                                                                                                                      Resultado:      18,18 s 363,6 m Puedes repetir el ejercicio pero suponiendo que ambos llevan el mismo sentido, d.    Cuanto tardará el que va más deprisa en atrapar al coche más lento? e.    En qué posición lo atrapará? f.      Representa las gráficas de los movimientos.                                                                                                                                                                                                                                                                                                                                         Resultado:      66,6 s 2.333,3 m 8.         Un coche sale de Girona hacia Cassà a 72 km/h; en el mismo momento una moto sale de Cassà para ir a Girona con una velocidad de 10 m/s. Entre Cassà y Girona hay 7,2 km. a.    Calcula la posición de ambos a los 2 minutos. b.    Calcula también su posición al cabo de 5 minutos. c.    Haz las gráficas x-t de los dos movimientos.                                                                                                                                                                                                                                                                                                             Resultado:       2.400 m y 6.000 m 6.000 m y 4.200 m 9.         A las 9 horas de la mañana pasa por una estación de servicio un vehículo robado con una velocidad constante de 90 km/h. A los diez minutos pasa por el mismo punto un coche de la policía persiguiendo al primero con una velocidad de 126 km/h. a.    Cuanto tiempo tardará la policía en detener a los ladrones? b.    En qué posición tendrá lugar la detención? c.    Haz las gráficas v-t y x-t de los dos coches.                                                                                                                                                                                                                                                                                                                                      Resultado:      1.500 s 52.500 m 10.     Girona y Castellón están separadas 360 km. Un tren sale de Girona hacia en Castellón con una velocidad de 108 km/h mientras que a la misma hora sale otro de Castellón pero con una velocidad de 72 km/h. a.    Cuanto tiempo tardaran en cruzarse los dos trenes? b.    En qué posición se encontrarán? c.    A qué distancia de Girona estarán entonces? d.    Y a qué distancia de Castellón?                                                                                                                                                                                                                                                                                                                                      Resultado:      7.200 s 216.000 m 216.000 m 144.000 m 11.     Dos personas que circulan con bicicleta salen de dos lugares separados 400 metros y llevan velocidades constantes de 5 m/s y 3 m/s. Han quedado en encontrarse en un punto entremedio. a.    Cuanto tiempo tardaran en encontrarse. b.    Donde se encontrarán? c.    Haz las gráficas v-t y x-t de los movimientos.                                                                                                                                                                                                                                                                                                                                              Resultado:      50 s 250 m 12.     En el momento de hacer un atraco, un ladrón es descubierto por un policía que se encuentra a 100 m de distancia . El ladrón sale corriendo a 18 km/h mientras que el policía lo persigue a 27 km/h. El ladrón tiene un cómplice con una moto a 300 m de distancia. Podrá el policía coger al ladrón? Encuentra la solución numérica y gráficamente.                                                                                                                                                                                                                                                                                                                  Resultado:       Sí, 300 m y 40 s 13.     El intrépido viajero Phileas Fogg, protagonista de "La vuelta al  mundo en 80 días" de Julio Verne, ha llegado tarde al puerto. El buque donde tenía que continuar el viaje hace dos horas que ha salido y va a 40 km/h. Pero Fogg no se da por vencido. Contrata los servicios de una pequeña motora y sale en persecución del barco a 50 km/h. a.    A cuantos kilómetros de la costa lo atrapará? b.    Cuanto tiempo tardará en pillarlo? Encuentra la solución numérica y gráficamente.                                                                                                                                                                                                                                                                                                                                      Resultado:      400 km 8 h OTRA SERIE DE EJERCICIOS: 3.         Di a qué tipo de movimiento corresponden las gráficas siguientes: 4.         (PAU septiembre 98) Es posible que la velocidad de un móvil sea negativa y su aceleración positiva? Si la respuesta es sí, pon un ejemplo; si es no, razónalo.   5.         Lanzo una bola por un plano inclinado: sube hasta que se para y después vuelve en bajar. a.    Haz las gráficas a-t, v-t y x-t aproximadas del movimiento. 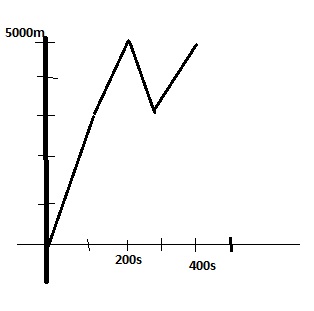6.         Dada la gráfica siguiente y sabiendo que el móvil sale del reposo, a.    Describe el movimiento b.    Haz, cualitativamente las gráficas v-t y x-t. c.    Calcula las velocidades finales de cada intervalo (suponiendo que inicialmente la velocidad es cero). d.    Calcula también las posiciones finales de cada tramo. e.    Representa, ahora cuantitativamente, las gráficas v-t y x-t. f.      Calcula la velocidad media a los 8 segundos y también a los 16 segundos.                                                                                                                                                                                                                                                                                                        Resultado:       4, 12, 12, 8 y 10 m/s 8, 40, 64, 104 y 122 m 5 m/s y 7,625 m/s 7.         Un móvil parte del reposo con una aceleración de 10 m/s2. a.    Construye las gráficas a-t, v-t y x-t. b.    Repite las gráficas considerando que la velocidad inicial es 5 m/s. 8.         Un coche que va a una velocidad de 108 km/h queda parado en sólo 5 segundos. a.    Calcula el espacio que necesita para frenar. b.    Haz las gráficas a-t, v-t y x-t del movimiento.                                                                                                                                                                                                                                                                                                                                            Resultado:       75 m 9.         Un móvil va a 72 km/h y frena con una aceleración de 2 m/s2. a.    Haz la gráfica v-t de su movimiento. b.    Calcula el tiempo que tarda en detenerse. c.    Qué espacio recorre antes de detenerse?                                                                                                                                                                                                                                                                                                                                            Resultado:        10 s 100 m 10.     Observa las gráficas siguientes. Tienes que sacar de cada una la máxima información posible del movimiento que representa. 11.     Un bloque se deja bajar por un plano inclinado de 2 metros de longitud. Tiene una aceleración constante de 4 m/s2. Cuando llega al final del plano inclinado continúa moviéndose con movimiento uniforme, con la velocidad que ha adquirido, sobre un plano horizontal hasta que choca y queda parado de golpe después de recorrer 2 metros más. a.    Calcula el tiempo que tardará en bajar el plano inclinado. b.    Calcula la velocidad que tendrá al término de la rampa. c.    Calcula el tiempo que tardará en chocar. d.    Haz las gráficas a-t, v-t y x-t del movimiento.                                                                                                                                                                                                                                                                                                                                                 Resultado:       1 s 4 m/s 1,5 s 12.     (PAU junio 98) El siguiente gráfico está referido a un móvil que describe un movimiento rectilíneo. Razona si las afirmaciones siguientes son verdaderas o falsas: a.    La gráfica corresponde a un movimiento uniformemente acelerado. b.    La aceleración en el punto t1 es positiva y en el punto t2 es negativa. 13.     (PAU junio 02) La figura representa la gráfica «velocidad - tiempo» para un cuerpo que se mueve sobre una recta y que sale del reposo. Razona si el espacio recorrido por el móvil en el intervalo de tiempo durante el cual aumenta su velocidad es mayor , más pequeña o al igual que el espacio recorrido durante la frenada.                                                                                                                                                                                                                                                                                                                                            Resultado:      igual 14.     Los siguientes datos corresponden a un movimiento uniformemente acelerado. Completa los datos que faltan en la tabla. t (s) 0 1 5 v (m/s) 20 24 x (m) 0 21 300 15.     Un coche que va a 36 km/h acelera durante 5 segundos hasta llegar a una velocidad de 108 km/h. Mantiene esta velocidad durante 20 segundos y después frena hasta detenerse en 10 segundos. a.    Calcula la distancia que habrá recorrido en total. b.    Haz las correspondientes gráficas a-t, v-t y x-t.                                                                                                                                                                                                                                                                                                                                         Resultado:       850 m 16.     Un bloque se deja deslizar con aceleración constante por un plano inclinado de 6 metros de longitud y tarda 2 segundos en bajarlo. Después continúa desplazándose en línea recta y velocidad constante por un plano horizontal de 4 metros. Finalmente sube por un plano inclinado (con un m.r.u.a.) y se para después de recorrer 3,6 m. a.    Construye las gráficas a-t, v-t y x-t del movimiento. 17.     Haz las gráficas a-t, v-t y x-t del siguiente movimiento: un coche que va a por la carretera Barcelona ve un semáforo rojo, frena y antes de detenerse el semáforo se pone verde, acelera y al cabo de un rato mantiene su velocidad constante. Al final frena hasta detenerse.   18.     Haz las gráficas a-t, v-t y x-t del movimiento del balón: 19.     Se llama tiempo de reacción al que transcurre desde que un conductor observa un obstáculo hasta que pisa el pedal del freno. Normalmente es de algunas décimas de segundo. Supon que la velocidad que lleva es de 90 km/h, el tiempo de reacción es de 0,4 segundos y que la aceleración de frenada es de -3 m/s2. a.    Calcula el espacio necesario para quedar parada. b.    Representa las gráficas a-t, v-t y x-t del movimiento.                                                                                                                                                                                                                                                                                                                                     Resultado:       114,1 m 20.     (PAU junio 01) La gráfica de la figura representa la velocidad en función del tiempo de un móvil que sale del origen de coordenadas y sigue un movimiento rectilíneo. Calcula: a.    La aceleración del móvil en el instante t = 20 s. b.    La distancia recorrida durante el movimiento de frenada. c.    En qué intervalo de tiempo su aceleración es máxima? Dibuja la gráfica x(t) para este intervalo.                                                                                                                                                                                                                                                                                                                                    Resultado:       0,5 m/s2 300 m 21.     (PAU septiembre 01) Una partícula sale del reposo y se mueve sobre una recta. En la gráfica adjunta se representa la aceleración de la partícula durante los 6 primeros segundos. Representa la gráfica v(t) del movimiento. 22.     Dos móviles se mueven en línea recta e inicialmente los dos están en la misma posición. El azul, que estaba parado, acelera de manera que después de un segundo ha recorrido 2 metros. Sabemos que ha seguido el trayecto con la misma aceleración. a.    Calcula la velocidad que lleva en los instantes 2, 3, 4 y 5 segundos. b.    En qué posiciones se encuentra en los mismos instantes?                                                                                                                                                                                                                                                                                                              Resultado:       8, 12, 16 y 20 m/s 8, 18, 32 y 50 m El rojo lleva desde el principio y durante todo el trayecto una velocidad constante y también hace 2 metros durante el primer segundo. c.    Calcula también su velocidad y posición durante los 5 primeros segundos. d.    En qué momento los dos coches llevan la misma velocidad?                                                                                                                                                                                                                                                                                                                                           Resultado:       2 m/s 0,5 s 23.     Un coche y un camión están separados 50 metros. El camión se mueve con una velocidad constante de 54 km/h mientras que el coche, que está inicialmente parado, arranca con una aceleración de 1,6 m/s2 que mantiene constante. a.    Cuanto tiempo tardará el coche en atrapar al camión? b.    En qué posición estarán entonces? c.    Qué velocidad llevará el coche en este instante? d.    Haz las gráficas a-t, v-t y x-t de los dos movimientos.                                                                                                                                                                                                                                                                                                                                         Resultado:       21,6 s 373,2 m 34,5 m/s 24.     Un peatón corre con la máxima velocidad posible a 6 m/s para coger una autobús que está parado en un semáforo. Cuando está a 25 metros el semáforo se pone verde y el autobús acelera uniformemente a razón de 1 m/s2. a.    Calcula el tiempo que tardará en atrapar el autobús, si es que no se le escapa. b.    Haz las gráficas a-t, v-t y x-t de los movimientos.                                                                                                                                                                                                                                                                                                                              Resultado:       No l'atrapa 25.     Dos coches circulan por el mismo carril pero en sentidos contrarios con velocidades de 90 km/h y 108 km/h. Cuando se divisan uno al otro están a 100 m de distancia y los dos comienzan a frenar con una aceleración de 5 m/s2. a.    Llegarán a chocar? b.    Si lo hacen, en qué posición tendrá lugar el impacto?                                                                                                                                                                                                                                                                                                                              Resultado:       Sí, chocan 44 m 26.     Un ciclista va a una velocidad constante de 6 m/s. Otro, que ha salido 16 m más atrás, acelera a 2 m/s2 hasta llegar a una velocidad de 8 m/s (que después mantiene constante). a.    Cuanto tiempo tardará en pillarlo? b.    En qué posición lo atrapará? c.    Haz las gráficas x-t y v-t de ambos ciclistas.                                                                                                                                                                                                                                                                                                                                               Resultado:      16s 112 m OTRA SERIE DE EJERCICIOS: 2.         Representa las gráficas a-t, v-t y x-t del movimiento de un objeto que lo lanzamos verticalmente y hacia arriba desde el suelo: sube, se para y vuelve en caer.  3.         (PAU junio 99) De un grifo gotean, separadas una de otra, dos gotas de agua. En un instante determinado, están separadas una distancia d. Razona si, con el paso del tiempo, mientras caen, esta distancia irá aumentando, menguando o permanecerá constante.  4.         Dejamos ir un objeto desde el terrado de un edificio y observamos que choca con el suelo al cabo de 2,5 segundos. a.    Con qué velocidad llega al suelo? b.    Cuál es la altura del terrado? c.    Haz las gráficas del movimiento.                                                                                                                                                                                                                                                                                                                                      Resultado:       -25 m/s 31,25 m 5.         Desde qué altura tiene que caer un objeto para que llegue al suelo con una velocidad de 100 km/h?                                                                                                                                                                                                                                                                                                                                        Resultado:      38,6 m 6.         Lanzamos un objeto desde el suelo hacia arriba con una velocidad de 25 m/s. a.    Qué velocidad y posición tiene al cabo de 2 segundos? b.    Puedes calcularlo también a los 4 segundos? c.    Cuanto tiempo tarda en llegar a la altura máxima? d.    Calcula la máxima altura a la que llega.                                                                                                                                                                                                                                                                                                                          Resultado:       5 m/s y 30 m -15 m/s y 20 m 2,5 s 31,25 m 7.         Un globo se encuentra a 80 m de altura. Cuanto tiempo tardará en llegar al suelo un objeto que dejamos caer desde el globo si: a.    el globo está parado. b.    el globo baja a 2 m/s. c.    el globo asciende a 2 m/s.                                                                                                                                                                                                                                                                                                                                                 Resultado:      4 s 3,80 s 4,20 s 8.         (PAU junio 99) Javier Sotomayor era el campeón de salto de altura con una marca de 2,45 m. Determina la velocidad con la que saltó verticalmente desde el suelo (velocidad de salida). Supon despreciables los efectos del rozamiento con el aire.                                                                                                                                                                                                                                                                                                                                           Resultado:       7 m/s 9.         Dejamos caer un objeto desde 10 metros de altura. a.    Con qué velocidad llega al suelo?                                                                                                                                                                                                                                                                                                                                 Resultado:       -14,1 m/s 10.     Al dejar caer un balón desde una ventana llega al suelo con una velocidad de 10 m/s. a.    Cuanto tiempo ha durado la caída? b.    A qué altura está la ventana? c.    Cuál es la velocidad media de la caída?                                                                                                                                                                                                                                                                                                                                                 Resultado:      1 s 5 m 5 m/s 11.     Un bombardero en picado baja verticalmente a 720 km/h y deja caer una bomba, que tarda 10 s en llegar al suelo. a.    Desde qué altura cae la bomba? b.    Con qué velocidad chocará con el suelo?                                                                                                                                                                                                                                                                                                             Resultado:       2.500 m ; 300 m/s 12.     Desde un puente lanzamos verticalmente y hacia arriba una piedra con una velocidad inicial de 12 m/s y tarda 3 segundos en llegar al río. a.    A qué altura máxima ha llegado la piedra? b.    Cuál es la altura del puente? c.    Con qué velocidad ha chocado con el agua? d.    Haz las gráficas a-t, v-t y x-t del movimiento.                                                                                                                                                                                                                                                                                                                                           Resultado:      7,2 m 9 m -18 m/s 13.     Desde 40 metros de altura lanzamos un objeto hacia abajo con una velocidad de 10 m/s. a.    Puedes saber el tiempo que tarde en caer? b.    Con qué velocidad choca con el suelo?                                                                                                                                                                                                                                                                                                                                                 Resultado:      2 s -30 m/s 14.     Dejamos caer una piedra. a.    Cuál es el espacio que recorre en los 4 primeros segundos? b.    Cuál es el espacio que recorre en los 4 segundos siguientes?                                                                                                                                                                                                                                                                                                                                            Resultado:      80 m 160 m 15.     Una persona desde arriba de un terrado a 30 m de altura lanza un balón hacia abajo con una velocidad de 5 m/s. En el mismo momento un compañero suyo lanza otro balón desde el suelo y hacia arriba con una velocidad de 30 m/s. a.    Puedes calcular en qué instante se encuentran los dos? b.    Sabes si se encuentran subiendo o bajando? c.    Cuál es la altura máxima de la segunda pelota? d.    Representa aproximadamente las gráficas x-t, v-t y a-t de los dos movimientos.                                                                                                                                                                                                                                                                                                                                         Resultado:      0,85 s Subiendo 45 m 16.     Un método que puede utilizarse para determinar la profundidad de una sima consiste en dejar caer una piedra y contar el tiempo que transcurre hasta que se oye el choque con el fondo. Suponemos que hemos oído el choque después de 4 segundos y no tenemos en cuenta la velocidad del sonido. a.    Cuál es la profundidad de la cueva?                                                                                                                                                                                                                                                                                                                                            Resultado:      80 m Si tenemos en cuenta la velocidad del sonido (340 m/s), b.    Cuál será ahora la profundidad de la sima?                                                                                                                                                                                                                                                                                                                                        Resultado:      71,7 m 17.     Dejamos caer un objeto desde 125 m de altura y después de 3 segundos lanzamos otro objeto. a.    Con qué velocidad tenemos que lanzar este objeto para que lleguen ambos al mismo tiempo al suelo. b.    Calcula la velocidad de cada objeto cuando llega al suelo.                                                                                                                                                                                                                                                                                                                                 Resultado:       -52,5 m/s -50 m/s y -72,5 m/s 18.     Desde qué altura dejamos caer una piedra si para hacer la primera mitad del trayecto tarda 5 segundos más que para hacer la segunda.                                                                                                                                                                                                                                                                                                                                     Resultado:      722,5 m 19.     Lanzamos una piedra desde el suelo hacia arriba con una velocidad de 30 m/s. Una persona que está dentro del edificio ve la piedra entre 1 s y 1,1 s después de haberla lanzado. a.    A qué altura está la ventana? b.    Qué dimensiones tiene la ventana (verticalmente)? c.    A qué altura llegará la piedra? d.    Haz las gráficas a-t, v-t y x-t del movimiento.                                                                                                                                                                                                                                                                                                                                            Resultado:      25 m 1,95 m 45 m 20.     Uno piedra en caída libre pasa por delante de un observador situado a 300 m del suelo. Al cabo de 2 segundos pasa por delante de otro observador situado a 200 m del suelo. Calcula: a.    Desde qué altura cae la piedra. b.    Cuando tarda en llegar al suelo desde que ha comenzado a moverse. c.    Con qué velocidad llega al suelo.                                                                                                                                                                                                                                                                                                                                         Resultado:      380 m 8,72 s -87,2 m/s 21.     (PAU junio 00) Desde una altura de 200 m sobre el suelo lanzamos verticalmente y hacia arriba un cuerpo con una velocidad inicial de 30 m/s. a.    Haz un dibujo aproximado de la gráfica velocidad-tiempo correspondiente al movimiento de este cuerpo desde el instante de lanzamiento hasta que llega al suelo (indica en el gráfico los valores de v y t correspondientes a los instantes inicial y final). Considera g = 10 m/s2 . b.    Cuanto tiempo tarda en recorrer los últimos 50 m? c.    Cuál será su posición respeto al suelo en el instante en que el cuerpo baja con una velocidad de módulo igual a 40 m/s?                                                                                                                                                                                                                                                                                                                                         Resultado:      0,76 s 165 m 22.     Lanzamos verticalmente hacia arriba dos objetos, con una velocidad de 100 m/s con un intervalo de 4 s. a.    Qué tiempo pasará desde el lanzamiento del primero hasta que se encuentren? b.    A qué altura se encuentran? c.    Qué velocidades tendrán en el momento de cruzarse?                                                                                                                                                                                                                                                                                                                                               Resultado:      12s 480m 20 y -20 m/s 23.     (PAU junio 03) Un cohete es lanzado verticalmente hacia arriba, desde el reposo, y sube con una aceleración constante de 14,7 m/s2 durante 8 s. En este momento se le acaba el combustible, y el cohete continúa su movimiento de manera que únicamente está sujeto a la fuerza de la gravedad. a.    Calcula la altura máxima a la qué llega el cohete. b.    Calcula el tiempo transcurrido desde la salida hasta la vuelta del cohete a la superficie de la tierra. c.    Haz un gráfico velocidad - tiempo de este movimiento. Considera g = 9,81 m/s2.                                                                                                                                                                                                                                                                                                                                      Resultado:      1175 m 35,47 s