Seguimos haciendo problemas de movimientos y hay van tres ejemplos resueltos:

4.         Un coche hace un trayecto según la siguiente gráfica v-t. Sabemos que en el instante inicial su posición es cero.

a.    Describe verbalmente el movimiento.

b.    Calcula la posición de este coche al término de cada intervalo de tiempo (siempre respecto al origen).

c.    Construye la gráfica posición-tiempo correspondiente.

d.    Cuál ha sido su desplazamiento?

e.    Qué velocidad media ha mantenido?

Observamos la gráfica. Sabemos que en el instante inicial la posición es x=0.

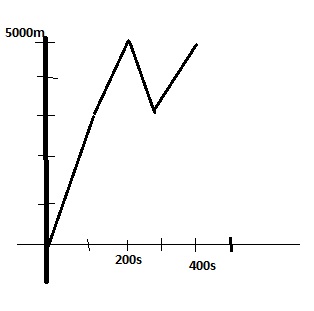
Durante 100 s lleva una velocidad 30, después 100s a 30, después 100 s a -20(vuelve hacia atrás)y después otros 100 s a 20. Es una sucesión de movimientos uniformes encadenados. No hay aceleración.

1 tramo:

x= xo + v.t = 0 + 100.30 = 3000m.   Esta fase acaba en 3000m

2 tramo:

x= xo + v.t = 3000 + 100.20 = 5000m.   Esta fase acaba en 5000m

3 tramo:

x= xo + v.t = 5000 + 100.(-20) = 3000m.   Esta fase acaba en 3000m

4 tramo:

x= xo + v.t = 3000 + 100.20 = 5000m.   Esta fase acaba en 5000m

9.         A las 9 horas de la mañana pasa por una estación de servicio un vehículo robado con una velocidad constante de 90 km/h. A los diez minutos pasa por el mismo punto un coche de la policía persiguiendo al primero con una velocidad de 126 km/h.

a.    Cuanto tiempo tardará la policía en detener a los ladrones?

b.    En qué posición tendrá lugar la detención?

c.    Haz las gráficas v-t y x-t de los dos coches.

Cuando sale el policía, el ladrón lleva 10 minutos de ventaja lo que es equivalente a 15 Km o 15000. La velocidades en m/s son 35 y 25. El policía irá recortando distancia hasta que alcance al ladrón. Escribirmos las ecuaciones del movimiento del ladrón y del policía (no tienen aceleración)

ladrón   x= 15000 + 25 t      policía  x= 0 + 35t    resolvemos el sistema:

t=1500s  y x= 52500m = 52,5 km

19.     Se llama tiempo de reacción al que transcurre desde que un conductor observa un obstáculo hasta que pisa el pedal del freno. Normalmente es de algunas décimas de segundo.

Supon que la velocidad que lleva es de 90 km/h, el tiempo de reacción es de 0,4 segundos y que la aceleración de frenada es de -3 m/s².

a.    Calcula el espacio necesario para quedar parada.

b.    Representa las gráficas a-t, v-t y x-t del movimiento.

En la primera parte de la frenada el conductor todavía no ha reaccionado. Durante 0,4 s, no frena y lleva movimiento uniforme.

Después pisa el freno y el coche pierde velocidad hasta que finalmente se detiene. En esta fase hay que calcular cuanto tiempo tarda en detener el coche y después podemos calcular la distancia recorrida.

1ºFase. 90 km/h= 25 m/s    x= 0 + 25. 0,4= 10 m  mientras reacciona

2º fase.  Tiempo que tarda en detenerse.  v= v0+at   

0 = 25 + (-3).t  t=8,3s

 y la posición final  x= xo + vm.t = 10 + (12,5).8,3 = 218 m

también lo podemos hacer con la fórmula x= xo + vo.t + 1/2.a.t2